Follow us on LinkedIn
The Black-Scholes-Merton model is one of the earliest option pricing models that was developed in the late 1960s and published in 1973 [1,2]. The most important concept behind the model is the dynamic hedging of an option portfolio in order to eliminate the market risk. First, a delta-neutral portfolio is constructed, and then it is adjusted to stay delta neutral as the market fluctuates. Finally, we arrive at a Partial-Differential Equation for the value of the option.
![]()
where
- V denotes the option value at time t,
- S is the stock price,
- r is the risk-free interest rate and,
- σ is the stock volatility.
This equation is also called a diffusion equation, and it has closed-form solutions for European call and put options. For a detailed derivation and analytical formula, see Reference [3].
In this post, we focus on the implementation of the Black-Scholes-Merton option pricing model in Python. Closed-form formula for European call and put are implemented in a Python code. The picture below shows the prices of the call and put options for the following market parameters:
- Stock price: $45
- Strike price: $45
- Time to maturity: 1 year
- Risk-free rate: 2%
- Dividend yield: 0%
- Volatility: 25%
![]()
We compare the above results to the ones obtained by using third-party software and notice that they are in good agreement.
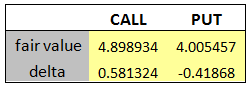
In the next installment, we will price these options using Monte Carlo simulation.
References:
[1] Black, Fischer; Myron Scholes (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy. 81 (3): 637–654
[2] Merton, Robert C. (1973). Theory of Rational Option Pricing. Bell Journal of Economics and Management Science.
[3] Hull, John C. (2003). Options, Futures, and Other Derivatives. Prentice Hall
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum

Citigroup on Friday posted second-quarter results that topped expectations for profit and revenue on a rebound in Wall Street activity.

JPMorgan Chase on Friday posted second-quarter profit and revenue that topped analysts' expectations as investment banking fees surged 52% from a year earlier.

NEW YORK — Announcement of Mesabi Trust Distribution The Trustees of Mesabi Trust (NYSE:MSB) declared a distribution of thirty cents ($0.30) per Unit of Beneficial Interest payable on August 20, 2024 to Mesabi Trust Unitholders of record at the close of business on July 30,…

