Delta hedging is a risk management strategy widely used in financial markets, particularly in options trading. The primary objective of delta hedging is to offset or neutralize the directional risk, or delta exposure, associated with an options position.
Delta represents the sensitivity of an option’s price to changes in the price of the underlying asset. To implement delta hedging, traders adjust their positions in the underlying asset (stocks, for example) to counterbalance the delta of the options they hold. If a trader is long an option with a delta of 0.6, indicating sensitivity to price changes, they might sell or short 60 shares of the underlying asset to create a delta-neutral portfolio. This dynamic strategy helps traders manage risk by mitigating potential losses due to changes in the underlying asset’s price, creating a more stable and predictable portfolio.
When delta hedging, a crucial question arises: how often should we hedge, and what volatility should we use to calculate the delta? Reference [1] investigates this question within the context of the oil market. The author pointed out,
It is not surprising that with less frequent hedging, the risks measured by the annualized standard deviation of the portfolio’s P&L steadily increase. More interesting is the observation that annualized profits also increase slightly if the portfolio does not rebalance the delta for at least two days. This confirms that some additional gains can indeed be captured from short-term price reversals by leaving the portfolio unhedged for a few days. If instead of hedging every day, the trader hedges only every two or three days, then higher profitability adequately compensates for taking larger risks while simultaneously saving on transaction costs. However, leaving the strategy unhedged for more than a week makes it less attractive on a risk-adjusted basis. While such a strategy allows traders to benefit from short-term price reversals, it can suffer significant losses if the portfolio is left unhedged for too long.
The findings are consistent with our intuitions: hedging less frequently increases PnL variance but decreases costs. There is, however, an interesting finding: hedging more frequently doesn’t yield the highest expected return. In other words, there exists an optimal hedging frequency that maximizes the expected return.
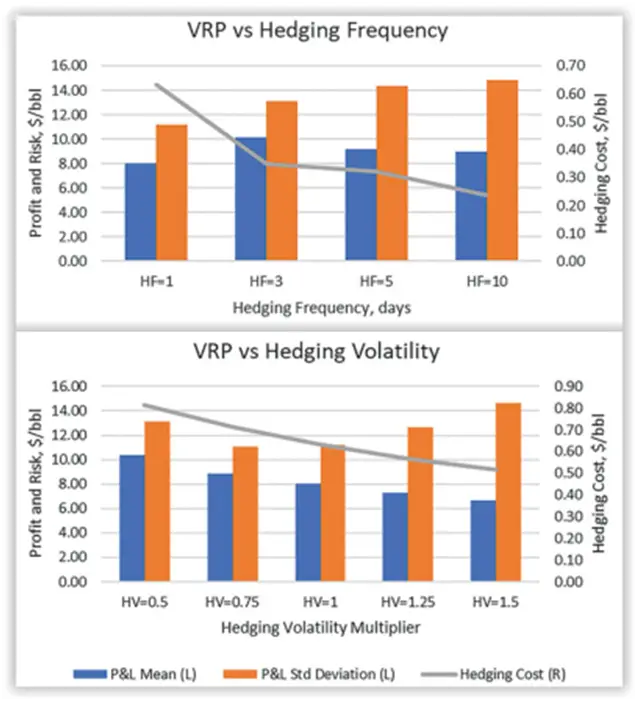
The author also explores different hedging volatilities,
To illustrate VRP sensitivity to the choice of the hedging delta, we scale the hedging volatility by multiples of 0.5, 0.75, 1.25, and 1.5 of the prevalent implied volatility. The multiple of 1.0 represents the base case. The results of this experiment are summarized in Fig. 9.10.
The most interesting takeaway from this analysis is P&L improvement from hedging with low volatility and P&L decline for hedging with high volatility.
In short, it’s not necessary to hedge using implied volatility. Opting for lower volatility in hedging results in a higher expected return.
These findings are insightful. It’s important to note, however, that they specifically pertain to short gamma positions. If you’re long gamma, the conclusions might differ.
Let us know what you think in the comments below or in the discussion forum.
References
[1] Bouchouev, I. (2023). The Art and Science of Delta Hedging. In: Virtual Barrels. Springer Texts in Business and Economics. Springer, Cham, pg. 202
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum
It was a Netflix documentary Michael Nantais watched during the early months of the pandemic that cemented his love of sustainable farming. Nantais, who grew up just outside of Montreal in Pointe-Claire, started experimenting in his mother’s backyard_ growing kale, cucumbers, and zucchinis for the…
