Follow us on LinkedIn
What is Normal Distribution?
A normal distribution is a probability distribution that is symmetric about the mean. It shows that data near the mean occur more frequently than data that exists far from it. Graphically, the normal distribution resembles the shape of a bell curve. It is a prevalent distribution assumed in performing a technical stock market or other types of statistical analysis.
In finance, the assumption of a normal distribution is common in asset prices and price action. Investors can plot price points over time to fit recent price action into a normal distribution. If the price action is further from the mean, it is more likely that an asset is over or undervalued. Investors can also use the standard deviation to suggest potential trades.
What is the Skewness of Normal Distribution?
The skewness of normal distribution refers to the asymmetry or distortion in the symmetrical bell curve for a given dataset. If a normal distribution’s curve shifts to the left or right, it is known as a skewed normal distribution. For any given distribution, its skewness can be quantified to represent its variation from a normal distribution.
For a normal distribution, the skewness will always be equal to zero. On the other hand, a log-normal distribution usually has a right-skew. A right-skew distribution is also known as a positively-skewed distribution. Similarly, the left-skew distribution is the opposite and is known as a negatively-skewed distribution.
Another characteristic of skewed distributions is the difference between the mean and median. For a right-skewed distribution, the mean will be greater than the median. Likewise, for a left-skewed distribution, the opposite is true. Similarly, for a normal distribution, the mean and median will be the same.
How to measure Skewness?
There are various ways to measure skewness. Among these, the most commonly used ones are Pearson’s mode and mean skewness. Pearson’s mode skewness subtracts the mode from the mean and divides the difference by the standard deviation to quantify skewness. In contrast, Pearson’s mean skewness deducts the median from the mean and multiplies the difference by three. Then it divides the product by the standard deviation.
How to apply skewness to portfolio return?
Investors use skewness to judge a return distribution as it considers the extremes of a dataset rather than focusing on the mean. Skewness is particularly useful for investors looking to invest in the short- or medium-term. These investors usually need to look at extremes as they are less likely to hold a position long enough to rely on the average working out. By looking at skewness, they can achieve that.
Similarly, investors use standard deviation to predict future returns. However, the standard deviation assumes a normal distribution. Since most return distributions don’t come close to a normal distribution, skewness represents a better measure to base performance predictions. Positively-skewed distributions usually imply numerous small negative returns and a few large ones.
Generally, investors prefer to invest in assets that have positive skewness. It is because these would trade at higher prices. Usually, investors are willing to pay premium prices for assets that have a return distribution concentrated on the positive side.
Conclusion
The skewness of distribution shows the asymmetry of the symmetrical bell curve for a given set of data. A normal distribution has a skewness of zero. However, asymmetrical distributions can have a positive or negative skew. Investors use skewness to evaluate their portfolio returns when making decisions.
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum
Meta rolled back January 6-era restrictions on former President Donald Trump's social media accounts ahead of the Republican National Convention.



June saw 75 filings, up from 62 in May and above the pandemic-era peak of 74 in July 2020, according to S&P Global Market Intelligence.
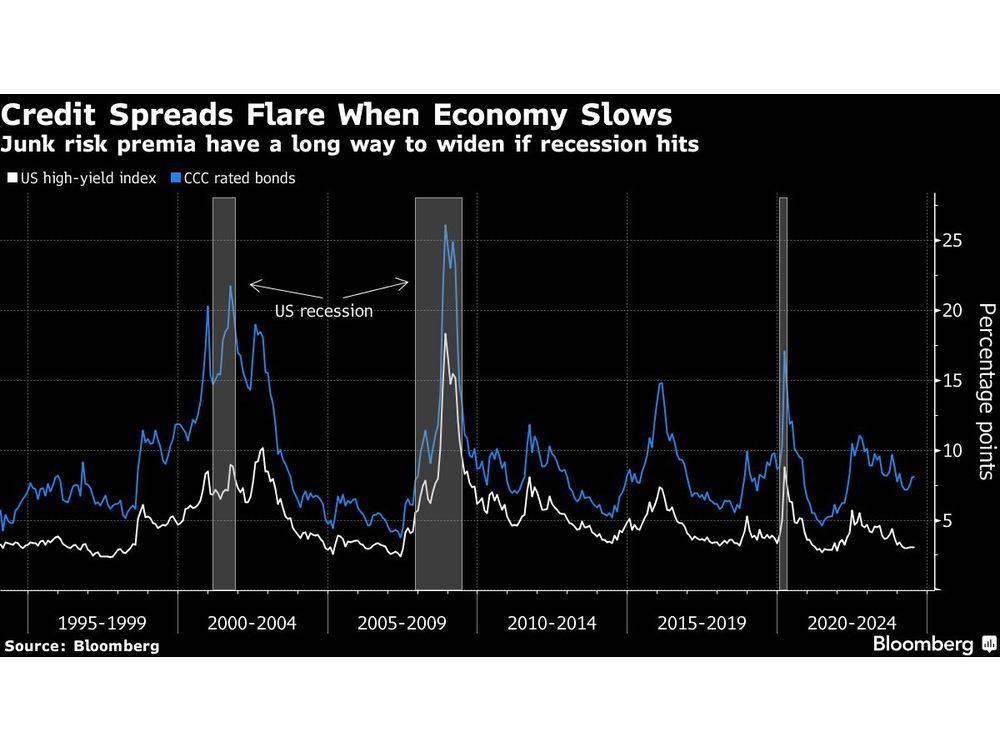
Credit markets are breathing a sigh of relief after inflation data showed price pressures are cooling broadly, but a weakening economy poses fresh risks to corporate debt.