Follow us on LinkedIn
Convertible bonds are complex securities that are part debt, part equity. The main feature of a convertible bond is the conversion that allows the bondholder to convert debt to equity. In addition, there can be many other “exotic” features such as callable, puttable, forced conversion, soft call, contingent conversion, etc.
Given their complexities, convertible bonds’ pricing is often very involved. A convertible bond is usually priced by using a lattice (binomial or trinomial tree) model or the Partial Differential Equation (PDE) approach. Another method is the Monte-Carlo simulation [1]. This method is less popular than the lattice or PDE approaches, but it has an advantage in that it can account for path-dependent features such as contingent conversion or 20/30 soft calls.
The pricing of a convertible bond under the Monte-Carlo approach starts with simulating the underlying price which is assumed to follow a Geometrical Brownian Motion. This is a common assumption in practice to model stock prices. The time to expiration is divided into equal time intervals; and in each time interval, the stock price is simulated using an exact scheme. This procedure generates price paths and we repeat it many times.
Since the conversion option can be exercised at any time during a given period, the valuation of a convertible bond is similar to that of an American option. Using dynamic programming principles, the value of a convertible bond can be determined recursively in a similar manner as in the tree or partial differential equation approaches.
Briefly, for each price path, the convertible bond’s continuation value is approximated using Least-Squares regression as suggested in the paper of Longstaff and Schwartz [2] for the valuation of the American option. The main steps involved in valuing a convertible bond using Monte Carlo simulation are as follows,
- Simulate the stock price.
- For each path, calculate the convertible bond value at maturity.
- Move on to the previous time step and calculate the continuation value using Longstaff and Schwartz scheme. Choose the first 4 Laguerre polynomials and a constant as basis functions [3].
- If the conversion is allowed, check if early exercise is optimal by comparing the continuation value to the conversion value. If early exercise is optimal, the cash flow at this time for this particular path is set equal to the conversion value, and all other cash flows afterward are set to nil.
- Continue in this manner backward until the inception.
- Finally, the value of the convertible bond given certain exercise strategies is determined by averaging the discounted cash flows of all the simulated paths.
This pricing method is more computationally involved than the lattice or PDE approaches. However, it offers greater flexibilities regarding the implementation of more complex, exotic features, especially path-dependent ones. Using this method, the precision of the pricing is approximately 0.5% of the convertible bond’s value.
References
[1] See for example M. Ammann, A. Kind, C. Wilde, Simulation-based pricing of convertible bonds, Journal of Empirical Finance 15 (2008) 310–331
[2] F. Longstaff and E. Schwartz, Valuing American options by simulation: A simple least-squares approach, Review of Financial Studies, Spring 2001, pp. 113–147.
[3] Other basis functions can also be used.
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum




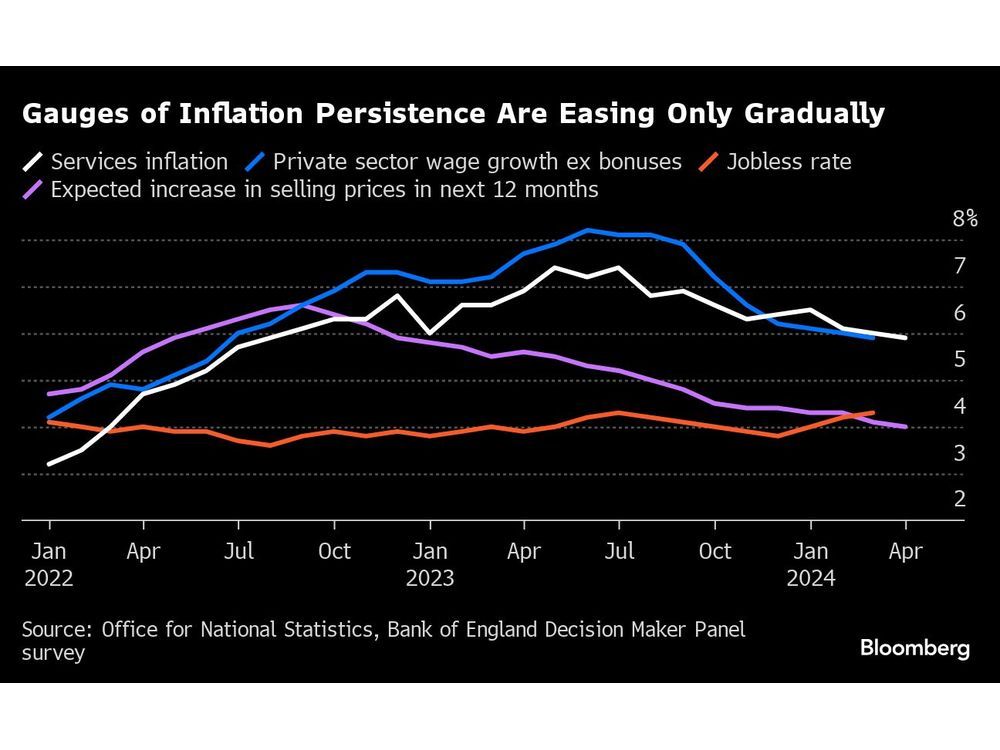
Prime Minister Keir Starmer’s promise to “get Britain building again” will quickly face a shortage of skilled workers in the very industries he’s hoping will power the turnaround.