Follow us on LinkedIn
Volatility measures market expectations regarding how the price of an underlying asset is expected to move in the future. There are two types of volatility: historical volatility and implied volatility. In a series of previous posts, we presented methods and provided Python programs for calculating historical volatilities. In this post, we are going to discuss implied volatility and provide a concrete example of implied volatility calculation in Python.
In financial mathematics, the implied volatility (IV) of an option contract is that value of the volatility of the underlying instrument which, when input in an option pricing model (such as Black–Scholes), will return a theoretical value equal to the current market price of said option. A non-option financial instrument that has embedded optionality, such as an interest rate cap, can also have an implied volatility. Implied volatility, a forward-looking and subjective measure, differs from historical volatility because the latter is calculated from known past returns of a security. To understand where implied volatility stands in terms of the underlying, implied volatility rank is used to understand its implied volatility from a one-year high and low IV. Read more
Since there is no analytical formula for calculating the implied volatility of an option, we must use numerical root-finding techniques. While there are many techniques for finding roots, two of the most commonly used are Newton’s method and Brent’s method. More details about these methods can be found in Reference [1].
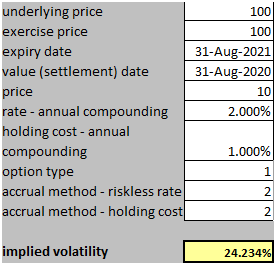
In this post, we utilize a Python program to calculate the implied volatility of a European call option. The parameters of the option are as follows.
Valuation date: August 31, 2020
Expiry: August 31, 2021
Option type: Call
Exercise type: European
Option price: 10
Strike: 100
Underlying asset price: 100
Risk-free rate: 2%
Dividend yield: 1%
The picture below shows the implied volatility calculated by the Python program.
![]()
We note that the implied volatility calculated by the Python program agrees well with the result obtained by using a third-party software as shown below.
References
[1] William H. Press, Saul A. Teukolsky, William T. Vetterling , Brian P. Flannery, Numerical Recipes 3rd Edition: The Art of Scientific Computing, Cambridge University Press, 3rd Edition, 2007.
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum




